5K Science Standards - 2021

Science Kit Inventory List

Kindergarten SC Performance Targets 

​Quarter At A Glance Document
​

You must be logged into @rhschools.org to access this folder.

Q1 At A Glance

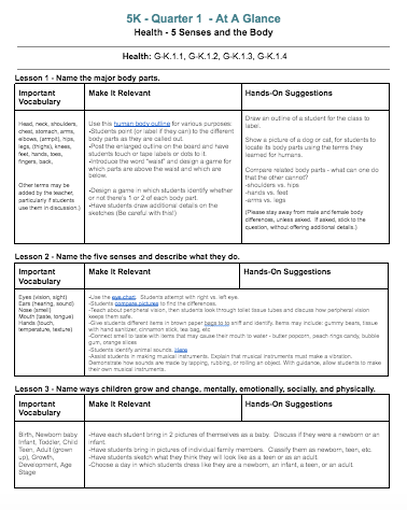
Q1 Standards

​Standards from SC Health Standards
(In prior years, 5K taught the 5 senses during Q1 for Science.  Now, during Q1 this unit will expand to 5 Senses and the Body from the SC Health Standards.  Additional info may be found at www.healthrockhill.weebly.com.) 
G-K.1.1 Name the major body parts. 
G-K.1.2 Name the five senses and describe what they do. 
G-K.1.3 Name ways children grow and change, mentally, emotionally, socially, and physically. 
​G-K.1.4 Explain how families are alike and different (e.g., several brothers and/or sisters; only one child; one parent working outside the home; a grandparent living in the home; pets or no pets).

---

Q2 At A Glance

Q2 Standards

​Science K-PS2-1  Plan and conduct an investigation to compare the effects of different strengths or different directions of pushes and pulls on the motion of an object.

K-PS2-2  Analyze data to determine if a design solution works as intended to change the speed or direction of an object with a push or a pull.

Health
I-J.1.1^  Identify ways to prevent common childhood injuries at home (e.g. falling down the stairs, drinking an unknown substance, finding a gun), school (e.g. climbing on playground equipment) of in the environment (running across the street, riding a bicycle, swimming, walking in a rainstorm, approaching an unknown animal)

---

Q3 At at Glance

Q3 Standards

​Standards from 2021 SC Science Standards
K-PS3-1  Make observations to determine the effect of sunlight on Earth’s surface.

K-PS3-2  Use tools and materials to design and build a structure that will reduce the warming effect of sunlight on an area.

K-ESS2-1 Use and share observations of local weather conditions to describe patterns over time.

K-ESS3-2 *Ask questions to understand the purpose of weather forecasting to prepare for and respond to severe weather

Standards from SC Health Standards
I-J.1.1^  Identify ways to prevent common childhood injuries at home

---

Q4 At A Glance

Order your Living Materials! 
Earthworms, Elodea, Snails, and Zebrafish

Q4 Standards

Standards from 2021 SC Science Standards

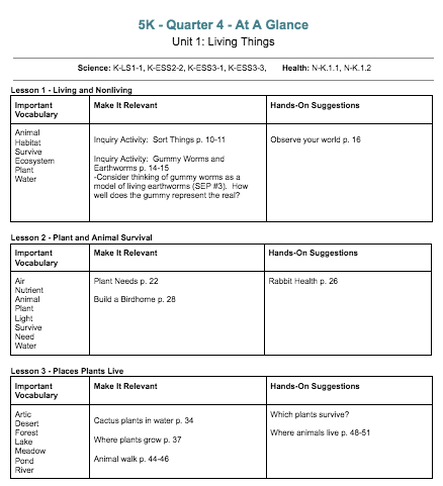
K-LS1-1  Use observations to describe patterns of what plants and animals (including humans) need to survive.

K-ESS2-2 Construct an argument supported by evidence for how plants and animals (including humans) can change the environment to meet their needs.

K-ESS3-1 Use a model to represent the relationship between the needs of different plants or animals (including humans) and the places they live.

K-ESS3-3  Plan and carry out an investigation that gives evidence of human impact on the land, water, air, and/or other living things in the local environment.

Health Standards
N-K.1.1 Explain why the body needs food, including breakfast, and water.

N-K.1.2 Define the terms healthy foods.

N-K.1.3 Explain why the body needs daily physical activity.

If you are planning to hatch chicks or ducks in your classroom, this link may help.